What is Quantitative Data?
A simple introduction and overview
In this article
- What is Quantitative Data?
- How to Collect Quantitative Data
- How to Measure Quantitative Data
- Quantitative Data Analysis
- Inferential Statistics
- Helpful References

Quantitative research involves the collection and analysis of data that can be quantified. Quantitative data is numerical in nature (i.e., involves numbers and varies in amount or quantity), is collected by directly measuring the variables of interest, and is typically analysed using statistical techniques. Quantitative data is often collected when researchers are interested in answering questions about ‘how much’ something differs or changes.
Types of Quantitative Data: Quantitative data can be broken down into two distinct types, and includes:
- Continuous data: Continuous data is data that is not limited to a specific number of responses or values, and can be reported in smaller units such as decimals or fractions. Continuous data can be further divided into interval or ratio data. Interval data occurs when data is labelled, the order of data is known, and the difference between data is also known. Interval data can contain a zero point, however zero in interval scales is often arbitrary. Ratio data is the same as interval data, however ratio data also features a ‘true zero’ point to indicate a total absence of what is being measured. Continuous data examples include height, weight, speed or distance.
- Discrete data: Discrete data is data that is limited to a specific number of responses. Discrete data is typically counted in whole numbers only, and can’t be broken down into smaller units such as decimals or fractions. Discrete data examples include the number of pairs of shoes someone owns, or the number of students in a class.
How to Collect Quantitative Data
There are a broad range of ways to collect quantitative data, however the specific methods of collection are dependent on two main factors – the study design that you are using to address your specific research question, and then what instruments or tools you are using to quantify the data within that specific design. For the former factor, several study designs can be applied to quantitative research, and can include:
| Type | Definition |
|---|---|
| Longitudinal | Examination of variables in a group of individuals over the course of a specified time frame, which allows for the quantification of your variables over time to see how they change. |
| Cross-Sectional | Examination of variables in a group of individuals at a specific point in time, which allows for the quantification of your variables at a fixed time point. |
| Case Study | In-depth investigations of variables in a small number of individuals. This allows for an in depth and more focused quantification of your variables. |
| Observational | A non-experimental study where the behaviour of individuals is observed/measured and recorded, and not changed or manipulated by a researcher. This allows you to quantify your variables in their natural state. |
| Experimental | The systematic, and tailored, manipulation and measurement of two or more variables to investigate how the change in one variable influences the other(s). |
| Correlational | Examination and quantification of a potential relationship between two variables, which demonstrates how one variable might relate to another. Read more about correlation coefficients |
How to measure quantitative data
How you measure quantitative data depends on your research question and associated variables of interest. Several methods can be used to quantify data, and can include:
| Type | Definition | |
|---|---|---|
| Questionnaires | A series of written and structured questions where participants are asked to choose from a series of answers. | |
| Interviews | A series of questions which are verbally communicated to the participants. Interviews can be structured, with the same questions asked of each participant, or unstructured, where there is no fixed structure. | |
| Experiments | Where, in a highly controlled environment such as a laboratory, researchers systematically manipulate one variable to investigate whether it causes a change in another. | |
| Controlled Observations | Where researchers observe participants in a controlled environment to see how they respond to certain situations. | |
| Direct Measurement | The use of specific and purpose-built tools to measure specific constructs directly, such as using a thermometer to measure temperature. | |
Quantitative Data Analysis
Since quantitative data relates specifically to numbers, to help understand what our data is saying, draw conclusions and therefore answer our research question we can analyse it using statistical techniques. The two main categories of statistics include descriptive and inferential types. The type of statistics that you use will depend on your research question.
Descriptive statistics help summarise the data you have collected, and allow for you to communicate the main features of your sample. Descriptive statistics include measures of central tendency and spread, which are often reported together. Measures of central tendency summarise the data to represent the centre of your sample, whereas measures of spread describe how much variability exists within your sample.
| Type | Definition | |
|---|---|---|
| Central Tendency | Mean | The typical, or average, score in a dataset. |
| Mode | The most frequently occurring score in a dataset. | |
| Median | The midpoint of a dataset. | |
| Spread | Range | The difference between the smallest and largest values in a dataset. |
| Quartiles and Interquartile Range | An index of variability in a dataset, where the data are divided into four parts (or quartiles) and then compared to one another to gauge where the scores are distributed. | |
| Standard Deviation | The most relied upon measure of variability which indexes by how much obtained scores differ from the mean of the dataset. | |
Inferential Statistics
Inferential statistics allow for researchers to draw conclusions about the broader population of interest. Inferential statistics allow for researchers to identify any significant differences, changes in or relationships between one or more samples and the broader population(s) which they were sampled from. Inferential statistics vary in complexity and the type of information they provide, but fall under the two main categories of parametric and non-parametric.
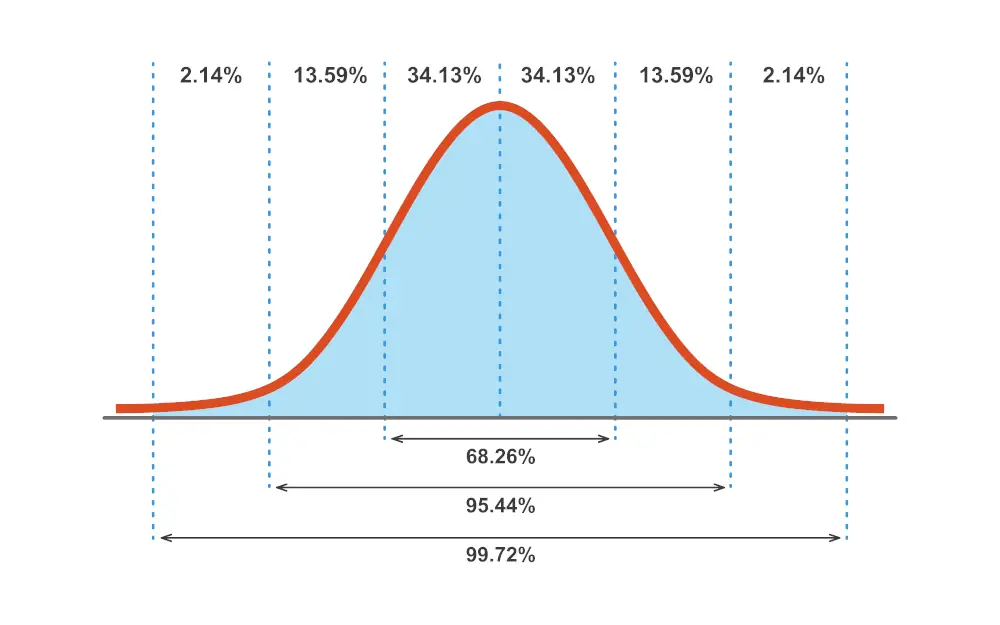 Graph of Normal Distribution
Graph of Normal Distribution
Parametric statistical tests assume that the data obtained come from a normally distributed population. When represented in a graph, a normal distribution looks like a bell shape where most of the scores are clustered around the mean and taper towards the ends. Common parametric inferential statistics include:
| Type | Definition | |
|---|---|---|
| One Sample Tests | One Sample Z Tests | A test used when you want to compare a sample to a known and defined population. This test is performed when you have one sample, and the population mean and standard deviation are known. |
| One Sample T Tests | Another test used when you wish to compare a sample to a known population, however not all the population parameters are known, and therefore must be estimated based on your sample. This test is performed when you have one sample, the population mean is estimated, but the population standard deviation is not known and must be estimated. | |
| Two Sample Tests | Two-Sample T Test |
Two Sample Tests Two-Sample T Test A test used to compare whether two population means are equal, and occurs in two forms: - An Independent Samples t Test tests if there is a difference between two separate groups. - A Correlated Groups t Test tests if there is a difference in the same group of participants. |
| Analysis of Variance (ANOVA) |
A test used to compare whether three or more population means are equal, and can include: - A Between-Subjects ANOVA tests whether there is a difference between three or more separate groups. - A Repeated-Measures ANOVA examines whether there is a difference in the same group of participants across three or more conditions. |
|
| Pearson Correlation | A test used to indicate whether a relationship between two variables exists, and if one does, index how strong that relationship is. | |
| Regression | A test used to examine whether one or more variables are associated with (or colloquially speaking, predicts) a particular outcome variable. | |
In contrast, non-parametric tests do not make the same assumptions about normality as parametric tests. When graphed, a non-parametric distribution does not look like a bell shape and typically has most of the scores closer to one end of the distribution. To address non-normality, non-parametric tests work by assigning each datapoint ranks and then analysing those. Common non-parametric inferential statistics include:
| Type | Definition |
|---|---|
| Mann-Whitney U Test | The non-parametric equivalent of an Independent Samples t Test. Aims to determine whether there is a difference in rank data between two separate groups |
| Wilcoxan Signed Rank Test | The non-parametric equivalent of a Correlated Groups t Test. Aims to determine whether there is a difference in rank data between two related groups (e.g. before/after). |
| Kruskal-Wallis H Test | The non-parametric equivalent of a Between-Subjects ANOVA. Aims to determine whether there is a difference in rank data between three or more separate groups. |
| Friedman’s ANOVA by Ranks | The non-parametric equivalent of a Repeated-Measures ANOVA. Aims to determine whether there is a difference in rank data between three or more related groups. |
| Spearman’s Rank Order Correlation | The non-parametric equivalent to a Pearson’s Correlation. Used to indicate whether a relationship between two non-normally distributed variables exists, and if one does, index how strong that relationship is. |
Helpful Resources
- Australian Bureau of Statistics (2021). Statistical Language – Quantitative and Qualitative.
- University of New South Wales (2021). Types of data & the scales of measurement.
- Simply Psychology. What’s the difference between qualitative and quantitative research?
- Wikipedia. Quantitative research